Für x und y sollen beliebige komplexe Zahlen zugelassen sein (die Null ausgenommen, da sie von vornherein ausscheidet). Alle x,y Î C können dann in der Form
dargestellt werden. Im Fall reeller und positiver (x,y) ist die Darstellung umkehrbar eindeutig und a,k Î R. Für Alle x,y Î C\R hat wegen der Beziehung ez = ez+2pi jedes x bzw. y unendlich viele Darstellungen.
Für die gesuchten Zahlenpaare ist demnach das logarithmische Verhältnis gleich dem gewöhnlichen Verhältnis. Setzen wir (1) in (2) ein, so ergibt sich
![]() ,
, ![]() ,
, ![]()
und damit ![]() , sowie
, sowie ![]()
. Mit ![]() erhalten
wir
erhalten
wir
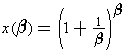 und
und 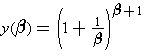 (3)
(3)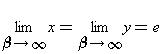 ist.
ist.
Wegen (3) gilt 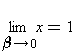 und
und 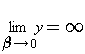 .
.
Jedem x Î R+ mit 1 < x < e ist aufgrund der Monotonie und der Stetigkeit der Funktion (3) genau ein y Î R+ zugeordnet mit e < y < ¥. Da x = 2 die einzige ganze positive Zahl zwischen 1 und e ist, ergibt sich, daß (2/4) das einzige Paar natürlicher Zahlen ist, welches potenzkommutativ ist.
Die nächste Aufgabe soll sein, die Gesamtheit aller rationalen potenzkommutativen Zahlenpaare zu ermitteln. Es ergibt sich sofort, daß
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Es gilt also z.B.![]() , was man durch elementare Umformung der Potenzen auch leicht nachrechnen
kann.
, was man durch elementare Umformung der Potenzen auch leicht nachrechnen
kann.
Wir zeigen nun, daß das für beliebige x Î
R+die einzigen rationalen Losungen sind. Wenn x und y beide
rational sind, muß auch ![]() und damit b rational sein. Sei also
und damit b rational sein. Sei also ![]() , mit p,q Î N und teilerfremd. Es gilt
dann
, mit p,q Î N und teilerfremd. Es gilt
dann
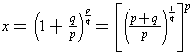 .
.x kann nur rational sein, wenn 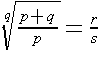 ,
mit r,s Î N, r > s
und r,s teilerfremd .
,
mit r,s Î N, r > s
und r,s teilerfremd .
daraus folgt p+q = rq ; p = sq
und rq = sq+q .
Sei r = s+k mit k Î N0
, dann gilt ( s+k)q = sq+q·sq-1·k+...+kq
= sq+q .
Diese Beziehung ist nur erfüllbar, wenn q = 1 und k = 1 . Somit
liefert b = p Î
N alle rationalen Lösungen.
Wenn b eine nicht ganze rationale Zahl ist,
erhält man für x und y algebraische irrationale Zahlen. Da jedem
x Î R mit 0 < x
< e , wie oben erläutert, genau ein y Î
R mit y > e zugeordnet ist, gibt es natürlich
Paare, bei denen die eine Zahl rational und die andere irrational ist.
In diesem Fall muß wegen ![]() die Zahl b irrational sein.
die Zahl b irrational sein.
Es sei noch erwähnt, daß es unter den Zahlenpaaren (x/y) genau eins gibt, bei welchem x und y im Verhältnis des goldenen Schnitts stehen. Und zwar ist dies der Fall, wenn
![]() bzw. b+1
= b2 gilt.
bzw. b+1
= b2 gilt.
Die positive Lösung ist bekanntlich die Verhältniszahl ![]() des goldenen Schnitts (der Major in bezug auf den Minor 1) . Die beiden
potenzkommutativen Zahlen sind dann xg = gg = 2,17845...
des goldenen Schnitts (der Major in bezug auf den Minor 1) . Die beiden
potenzkommutativen Zahlen sind dann xg = gg = 2,17845...
und yg = gg+1 = 3,52481... .
Das Besondere dieser beiden Zahlen ist, daß sowohl ihr gewöhnliches Verhältnis als auch ihr logarithmisches Verhältnis gleich g ist und zwar zu jeder beliebigen Basis:
Als Folge dieser Beziehungen gelten eine Reihe merkwürdiger Gleichungen, von denen wir hier einige aufführen.