[aus dem Forschungs- und Tätigkeitsbericht der Mathematisch-Astronomischen Sektion am Goetheanum 1992-1995, Freie Hochschule für Geistewissenschaft, CH-4143 Dornach, Schweiz]

Der momentane Bewegungszustand eines starren Körpers im Raum kann in jedem Zeitpunkt durch eine Schraubenbewegung dargestellt werden. Man spricht von einer "tangierenden Schraubenbewegung" , die in eine reine Drehung oder in eine Translation ausarten kann. Im nicht ausgearteten Fall bewegen sich also die Punkte des Raums auf Archimedischen Schraubenlinien mit gleicher Ganghöhe  2pk  um eine Achse h. Dabei ist es für den hier betrachteten Zusammenhang von fundamentaler Wichtigkeit, daß es bei gleicher Ganghöhe Links- und rechtsgewundene Schraubenlinien gibt, die nicht durch eine Bewegung ineinander übergeführt werden können, sondern nur durch eine Spiegelung. 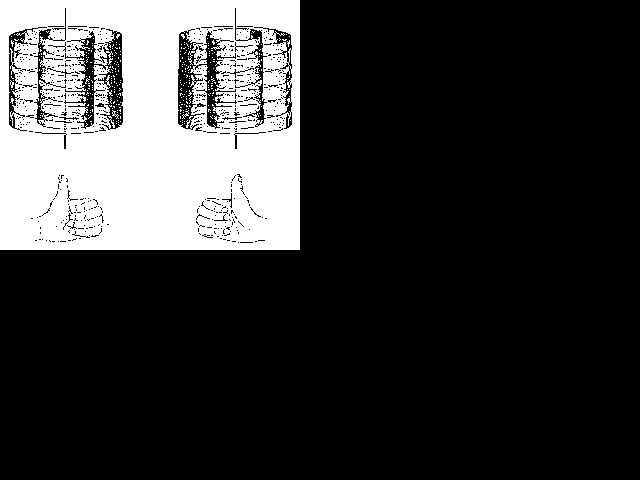Im üblichen rechtshändigen Koordinatensystem ist bei einer Rechtsschraube k > 0 und bei einer Linksschraube k < 0 (Abb.1).
 

Abbildung 1 Was man unter "linksgewunden" und "rechtsgewunden" verstehen soll kann man nicht mathematisch festlegen, sondern man muß dazu einen Gegenstand vorzeigen. Man kann es sich so merken: der Daumen zeige die fortschreitende Richtung und die leicht gekrümmten Finger die Drehrichtung. Nimmt man hierbei die rechte Hand, so erhält man eine Rechtsschraube, entsprechend mit der linken Hand eine Linksschraube. Korkenzieher, Schrauben und Gewinde (außer bei der Gasflasche) sind rechtsgewunden.

Statt durch die Schraubung kann man den momentanen Bewegungszustand eines starren Körpers auch durch den zugehörigen linearen Komplex beschreiben, einem Gebilde der höheren Liniengeometrie (vgl. ZIEGLER [4] ). Die Gesamtheit der linearen Komplexe bildet einen fünfdimensionalen projektiven Raum. Geht man von der Geschwindigkeit als der primären Qualität aus, so wird eine beliebige Bewegung eines starren Körpers durch eine Bahn in diesem Komplexraum beschrieben. Die Elemente dieser Bahn sind aber keine Raumpunkte sondern Geschwindikeitszustände. Nur wenn deren Gestalt sich ändert, ergibt sich eine Bahnkurve, ansonsten ein festes Element. Die Bahn als Ganzes beschreibt gewissermaßen die Gestalt der Änderung des Entsprechenden Bewegungsvorgangs.

Diese Zusammenhänge sind seit über 100 Jahren bekannt und untersucht worden. G. ADAMS [1] stellte sie in seiner Schrift "Universalkräfte in der Mechanik" zusammenfassend dar und zeigte, wie dadurch ganz neue Sichtweisen in der Mechanik gewonnen werden können. Daran knüpfen wir mit den folgenden Ausführungen unmittelbar an. ADAMS nennt den fünfdimensionalen Komplexraum "Urschraubenraum" und führt aus: "Die vierfach unendlich vielen Linien des dreidimensionalen Urraums sind ein Besonderes innerhalb des Urschraubenraums. Es sind "entartete" Urraumschrauben. Das links- und rechtshändig Schraubende erstirbt gleichsam in die ruhend-sichtbaren Linien hinein." ( ADAMS [1], §67 ) Zum Verständnis der vorliegenden Darstellung ist diese Sichtweise von grundlegender Bedeutung. Wenn man den Bewegungszustand als das Primäre nimmt, muß man den Komplex als eine intensiv gedachte Entität in einem fünfdimensionalen Gebiet denken, die Gestalt der sich ändernden Bewegung als ein Geschehen außerhalb des gewöhnlichen ruhend gedachten dreidimensionalen Raumes! P. GSCHWIND [3] spricht von "Geschwindigkeitsbereich" und zeigt, wie "es mit geeigneten Mitteln der synthetischen projektiven Geometrie möglich ist, im Denken zum Begriff einer Geschwindigkeit vorzustoßen, der nicht an ein räumlich-zeitliches Umfeld des Menschen gebunden ist, sondern der unabhängig von Distanzvorstellungen und vorgegebenen Zeiten irgendwelcher Art zu fassen ist und der zusätzlich viel allgemeiner ist als der physikalische." ( GSCHWIND [3], S. 125 )

Wenn man den Gedanken des Geschwindigkeitsbereichs als der primären Realität ernst nimmt, dann ist im Fall der Erdbewegung zunächst ihre Gestalt in diesem fünfdimensionalen projektiven Raum zu ermitteln. Im zweiten Schritt ist diese Gestalt in den "sichtbaren" Linienraum zu projizieren. Man erhält dann ein räumliches Bild dieser Bewegungsgestalt.

Auf die Einzelheiten der Projektion kann hier nicht eingegangen werden. Es ergibt sich jedenfalls eine "natürliche" Art von Projektion, die der stereographischen Projektion der Elementargeometrie entspricht. Wenn man das übliche Bild der Erde um die Sonne und die tägliche Drehung zusammen nimmt ergibt sich eine Schraubenbewegung die laufend die "Stärke" ihrer Windung ändert und jeweils ein halbes Jahr links- bzw. rechtsgewunden ist. Der Wechsel erfolgt am 21. Dezember und am 21. Juni. Beschreibt man, wie oben angedeutet, diese Bewegungsgestalt als Bahn im fünfdimensionalen Geschwindigkeitsbereich, so erhält man als Projektion der Erdbewegung eine sogenannte lemniskatische Regelfläche mit zwei reellen Leitgeraden (Abbildung 2).

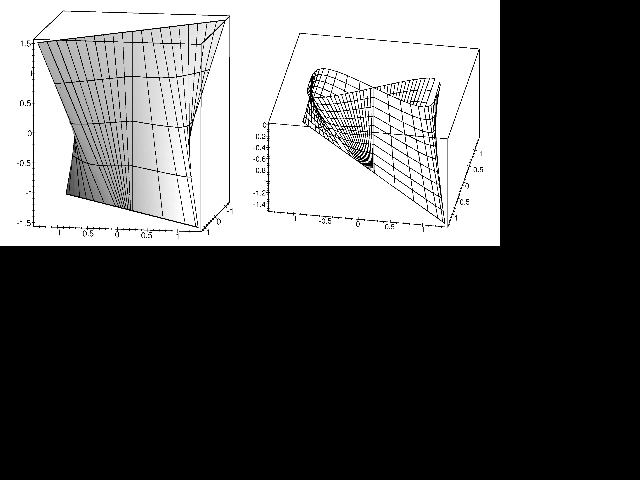
Abbildung 2 Lemniskatische Regelfläche mit zwei reellen Leitgeraden.
( G. ADAMS behandelt in [2] lemniskatische Regelflächen mit zwei konjugiert-imaginären Leitgeraden )

Man kann die Fläche auch folgendermaßen erzeugen: eine Gerade gleite an zwei festen windschiefen Leitgeraden l₁ und l₂ so entlang, daß sie gleichzeitig einen Kegelschnitt trifft, der in einer Ebene durch eine Treffgerade g von l₁ und l₂ liegt. Die Abbildung 2 zeigt eine besonders regelmäßige Form der entstehenden Fläche.
 

Schneidet man sie mit einer Ebene parallel zu den Leitgeraden, so erhält man eine lemniskatische Kurve 4. Ordnung. Ihre Gleichung hat die Form  (x2 - y2)2 - a2x2 + b2y2 = 0 .  Sie besitzt einen regulären Doppelpunkt und zwei reelle Doppelpunkte im Unendlichen, die Einsiedler sind. Wir nennen diese Kurvenschar hyperbolische Lemniskaten von Booth. Abbildung 3 zeigt die Gestalt der Kurve für verschiedene Werte von a. Die gewöhnliche Bernoullische Lemniskate würde man erhalten, wenn die lemniskatische Regelfläche zwei konjugiert-imaginäre Leitgeraden hätte.

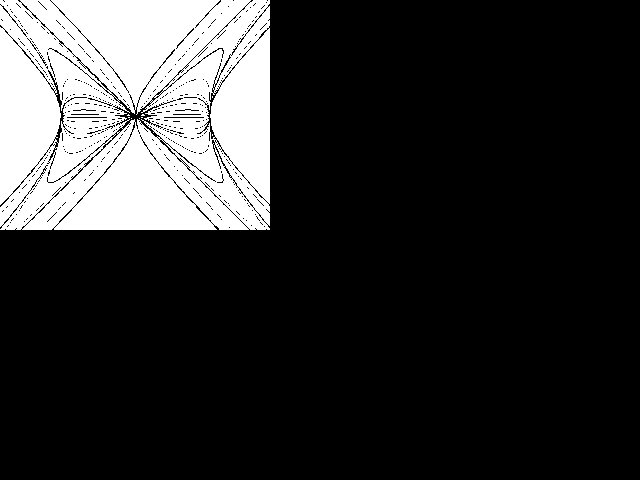
Abbildung 3  hyperbolische Lemniskaten von Booth

Das Interessante: jede Gerade, die nicht durch den Himmelspol oder den Pol der Ekliptik geht, kann als "Projektionszentrum" genommen werden und das Bild ist jedesmal lemniskatisch, sozusagen von jedem Blickwinkel im Geschwindigkeitsraum aus. Die Bahnkurve ² ist nicht nur qualitativ lemniskatisch, weil sie die zwei Seiten des Raumes durchläuft (im Sinne von Adams "lemniskatischer Natur des Raumes"), sondern ihre Projektion in den Linienraum ergibt auch eine unmittelbar lemniskatische Figur. Das Doppelelement g kann dabei eine ganz beliebige Lage haben, je nach "Blickwinkel". Legt man z.B. die Gerade g durch den Frühlings- und Herbstpunkt, so entspricht der Doppelpunkt der Lemniskate diesen Zeitpunkten.

Nimmt man noch die Verschiebung des Frühlingspunkts hinzu, so entsteht eine fortschreitende Lemniskate und zwar so, daß der Doppelpunkt der jährlichen Lemniskate in einem platonischen Weltenjahr selber eine Lemniskate durchläuft - ein sehr bemerkenswertes Ergebnis.

_________________________________

[1] ADAMS, GEORGE: Universalkräfte in der Mechanik, Dornach 1996
[2] ADAMS, GEORGE: Lemniskatische Regelflächen, Dornach 1989
[3] GSCHWIND, PETER: Raum, Zeit, Geschwindigkeit, Dornach 1986
[4] ZIEGLER, RENATUS: Höhere Liniengeometrie, Dornach1981

[ein ausführliches Manuskript ist in Arbeit]

homepage.d.koetter